- מְחַבֵּר Matthew Elmers [email protected].
- Public 2023-12-16 22:09.
- שונה לאחרונה 2025-01-24 09:25.

מה קובע דיוק - אחד המאפיינים העיקריים של נשק? ברור, מאיכות החבית והמחסנית. בוא נדחה את המחסנית לעת עתה, אך נשקול את הפיזיקה של התהליך.
קח מוט מתכת או צינור עשוי מתכת אלסטית ותקן אותו בנוקשות בבסיס מסיבי. אז אנו מקבלים דגם של המכשיר הנחקר. עכשיו, אם נפגע במוט, אין זה משנה באיזה מקום ובאיזה כיוון, או למשוך אותו לאחור, או לסחוט אותו, או, לבסוף, להכניס מחסנית לצינור ולירות ירייה, נראה שהמוט (חבית) נכנסה לתנועה תנודה לחה. תנודות אלו מתפרקות לפשוטות ביותר, וכל סוג של רטט כל כך פשוט של הקנה ישפיע על הדיוק (דיוק) הירי בדרכו שלו.
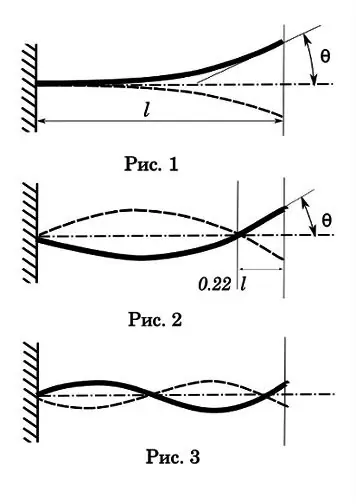
נתחיל ברטט מסדר ראשון או המגרש. כפי שאתה יכול לראות (איור 1), לתנודה כזו יש רק צומת אחד בנקודת ההתקשרות, המשרעת הגדולה ביותר, זמן הריקבון הארוך ביותר וזמן התנודה הארוך ביותר של תקופה אחת. הזמן הוא 0.017-0.033 שניות. זמן הנסיעה של הכדור דרך הקידוח הוא 0, 001-0, 002 שניות. כלומר, פחות משמעותית ממחזור של תנודה אחת, מה שאומר שלסוג זה של תנודה אין השפעה משמעותית על הדיוק של זריקה אחת. אך עם צילום אוטומטי יכולה להתברר תמונה מעניינת. נניח שקצב האש הוא 1200 rds / min, כלומר זמן של מחזור אחד - 0.05 שניות. עם תקופת תנודה ממדרגה ראשונה של 0, 025 שניות, יש לנו יחס תדרים מרובה. וזהו תנאי הכרחי לתהודה עם כל ההשלכות שלאחר מכן - הנשק מתחיל לרעוד בכוח כזה שהוא יכול להתפרק.
נעבור לתנודות בסדר השני (איור 2). אבל אני מציע שתלמידי מדעי הרוח יערכו תחילה ניסוי על מנת לחסל את חסרונות החינוך בתחום הפיזיקה. אתה צריך לקחת ילד קטן (אתה יכול ילדה), לשים אותו על נדנדה ונדנדה. לפניך מטוטלת. עמד בצד הנדנדה ונסה להכות את הילד בכדור. לאחר שורה של ניסיונות, תגיע למסקנה כי הדרך הטובה ביותר לפגוע היא כאשר המטרה נמצאת בשלב התנודה הראשון - הסטייה המרבית מנקודת שיווי המשקל. בשלב זה, למטרה יש מהירות אפס.
בואו נסתכל על תרשים הסדר השני. צומת הרטט השני ממוקם בערך 0.22 מקצה החבית. נקודה זו היא חוק טבע, אי אפשר ליצור רעידות כאלה לקרן השלוחה כך שהצומת השנייה תיפול על הקצה החופשי. הוא נמצא במקום ואינו תלוי באורך החבית.
משרעת התנודות עבור ערכת הסדר השני נמוכה יותר, אך זמן התנודה כבר דומה לזמן מעבר הכדור דרך הקידוח-0, 0025-0, 005 שניות. אז לצילום בודד זה כבר מעניין. כדי להבהיר על מה אנחנו מדברים, דמיינו חבית באורך 1 מטר. הכדור עובר בכל החבית תוך 0, 001 שניות. אם תקופת התנודה היא 0.004 שניות, אז עד שהכדור יעזוב את החבית, החבית תגיע לעיקול המרבי שלה בשלב הראשון. השאלה למדעי הרוח היא - באיזו נקודה (באיזה שלב) עדיף לירות כדור מהחבית כדי להבטיח עקביות של התוצאות? זכור את הנדנדה. בנקודת האפס, הווקטור של מהירות הסטת תא המטען הוא מרבי. קשה יותר לכדור לפגוע בנקודה זו בחיתוך החבית, יש לה גם טעות משלה במהירות. כלומר, הרגע הטוב ביותר עבור הכדור לעוף החוצה יהיה כאשר החבית נמצאת בנקודה הגבוהה ביותר של שלב ההסטה הראשון - כמו באיור.אז יופצו סטיות לא משמעותיות במהירות הכדור על ידי הזמן הארוך יותר שהקנה השלב בשלב היציב ביותר שלו.
ניתן לראות בבירור בתרשים ייצוג גרפי של תופעה זו (איור 4-5). כאן - Δt היא שגיאת הזמן שבה הכדור חוצה את לוע החבית. באיור. 4 אידיאלי כאשר זמן ההמראה הכדור הממוצע עולה בקנה אחד עם שלב האפס של תנודת החבית. (מתמטיקאים! אני יודע שהתפלגות המהירות היא לא לינארית.) האזור המוצל הוא זווית ההתפשטות של המסלולים.
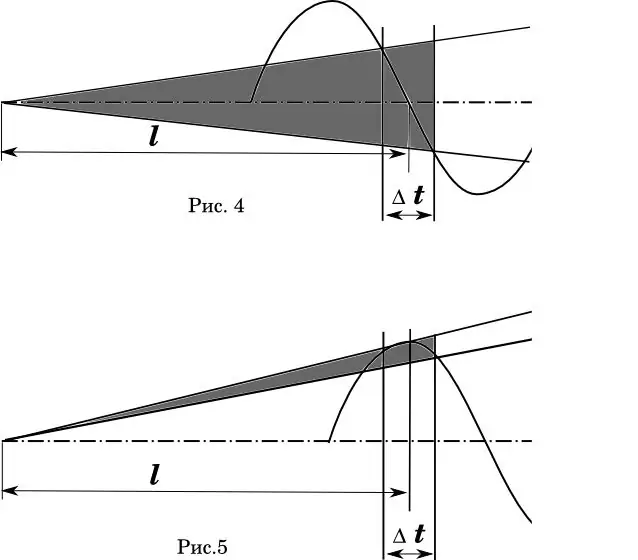
באיור 5, אורך החבית ושגיאת המהירות נשארים זהים. אך שלב כיפוף החבית משתנה כך שזמן היציאה הממוצע עולה בקנה אחד עם הסטה המרבית של החבית. האם הערות מיותרות?
ובכן, האם זה שווה את הנר? עד כמה החריגות יכולות להיגרם כתוצאה מתנודות מסדר שני? רציני ורציני מאוד. לדברי הפרופסור הסובייטי דמיטרי אלכסנדרוביץ 'ונטזל, באחד הניסויים התקבלו התוצאות הבאות: רדיוס החריגה החציונית גדל ב -40% עם שינוי באורך החבית ב -100 מ מ בלבד. לשם השוואה, עיבוד חבית איכותי יכול לשפר את הדיוק ב -20%בלבד!
עכשיו בואו נסתכל על הנוסחה לתדר הרטט:
איפה:
k - מקדם לתנודות מסדר שני - 4, 7;
L הוא אורך החבית;
E הוא מודול הגמישות;
אני רגע האינרציה של הקטע;
m הוא המסה של תא המטען.
… והמשך לניתוח ולמסקנות.
המסקנה המתבקשת מאיורים 4-5 היא שגיאת מהירות כדור. זה תלוי באיכות האבקה ובמשקל שלה וצפיפותה במחסנית. אם השגיאה הזו היא לפחות רבע מזמן המחזור, אפשר לוותר על כל השאר. למרבה המזל, המדע והתעשייה השיגו יציבות רבה מאוד בנושא זה. ולמתוחכמים יותר (במשענת ספסל למשל) יש את כל התנאים להרכבה עצמית של מחסניות על מנת להתאים את שלב השחרור של הכדור בדיוק לאורך הקנה.
אז, יש לנו מחסנית עם וריאציה המהירות הנמוכה ביותר האפשרית. אורך החבית חושב על סמך משקלו המרבי. עולה שאלת היציבות. אנו מסתכלים על הנוסחה. אילו משתנים משפיעים על השינוי בתדירות התנודה? אורך החבית, מודול הגמישות והמסה. החבית מתחממת במהלך הירי. יכול לשנות חום את אורך החבית כך שהדיוק יושפע. כן ולא. כן, מכיוון שנתון זה נמצא בתוך מאיות האחוזים לטמפרטורה של 200 C. לא. מכיוון שהשינוי במודול האלסטי של הפלדה לאותה טמפרטורה הוא בערך 8-9%, עבור 600C הוא כמעט פעמיים. כלומר הרבה יותר גבוה! החבית הופכת רכה יותר, שלב הכיפוף של החבית זז קדימה ברגע שהכדור עוזב, הדיוק יורד. ובכן, מה אומר אנליסט מתחשב? הוא יגיד שאי אפשר להשיג דיוק מרבי באורך חבית אחת במצב קר וחם! לנשק יש ביצועים טובים יותר עם חבית קרה או חמה. בהתאם לכך, מתקבלות שתי סוגי נשק. האחד מיועד לפעולות מארב, כאשר המטרה חייבת להיפגע מהזריקה הראשונה - "קרה", כי הדיוק של השנייה יהיה גרוע יותר בגלל החימום הבלתי נמנע של הקנה. בנשק כזה אין צורך דחוף באוטומציה. והמחלקה השנייה היא רובים אוטומטיים, שאורך החבית שלהם מותאם לחבית החמה. במקרה זה, אפשר לפצות על החמצה אפשרית עקב הדיוק הנמוך של זריקה קרה על ידי זריקה חמה ומדויקת מהירה שלאחר מכן.
EF Dragunov הכיר היטב את הפיזיקה של תהליך זה כאשר תכנן את הרובה שלו. אני מציע שתכיר את סיפורו של בנו אלכסיי. אבל ראשית, מישהו יצטרך לשבור את מוחו. כידוע, שני דוגמאות של קונסטנטינוב ודרגונוב ניגשו לגמר התחרות על רובה צלפים. המעצבים היו חברים ועזרו אחד לשני בכל דבר. אז הרובה של קונסטנטינוב "מכוון" למצב קר, הרובה של דראגונוב ל"חם ". מנסה לשפר את הדיוק של רובה היריבה, דראגונוב יורה ברובה שלו בהפסקות ארוכות.

בואו נסתכל על הנוסחה שוב.כפי שאתה יכול לראות, התדירות תלויה גם במסת החבית. מסת תא המטען קבועה. אך מגע קשה עם החזית מייצר משוב חיובי בלתי צפוי לחבית. המערכת-חבית-קצה-זרוע (תמיכה) תהיה בעלת רגע אינרציה שונה (קבוצת המונים ביחס לנקודת ההתקשרות), מה שאומר שזה יכול לגרום גם לשינוי פאזה. זו הסיבה שהספורטאים משתמשים בתמיכה רכה. אותה תכונה קשורה ביישום העיקרון של "חבית תלויה", כאשר לקדמת הנשק אין מגע קשה עם הקנה והוא מחובר אליו בצורה קשיחה (הנשק) רק באזור המקלט, והקצה השני או שאינו נוגע בחבית כלל או נוגע במפרק בעל קפיץ (SVD).
מחשבה אחרונה. העובדה שעם אותו חבית אי אפשר להשיג את אותו הדיוק בטמפרטורות שונות נותנת סיבה מצוינת למתוח את המוח. יש צורך לשנות רק את אורך ו / או המסה של החבית כאשר טמפרטורת החבית משתנה. בלי לשנות לא את האורך או את המשקל של החבית. מנקודת המבט של מדעי הרוח, זהו פרדוקס. מנקודת מבטו של טכנאי, משימה אידיאלית. כל חייו של מעצב קשורים לפתרון בעיות כאלה. שרלוקס נח.






